Understanding The Trapezoid Area Formula - A Simple Guide
Figuring out the space a shape takes up can feel like a bit of a puzzle sometimes, especially when you're looking at something that isn't just a plain square or a simple triangle. Yet, there are some pretty neat ways to measure even the most interesting forms. One shape that comes up quite a bit, in all sorts of places from architecture to crafts, is the trapezoid. It’s that four-sided figure with just one pair of sides running perfectly alongside each other, kind of like a table with a wider top than its bottom, or a window that narrows as it goes up. So, if you’ve ever wondered how to measure the surface inside one of these, you’re in for a treat, because there's a straightforward method that makes it quite clear.
When you’re thinking about how much room something occupies, whether it's a piece of land shaped like this or a design element in a building, knowing how to measure its flat surface is, you know, really useful. The way we figure out the space within a trapezoid, its area, is actually pretty logical once you get the hang of it. It involves just a few key measurements, and then you put them together in a particular order. It’s not nearly as complicated as it might seem at first glance, and honestly, it’s a tool that can help you look at the world around you with a slightly different perspective, seeing geometry everywhere.
This simple approach to finding the area of a trapezoid, or the amount of flat ground it covers, is something that, like, many people find helpful. It’s a fundamental idea in geometry, which is the study of shapes and spaces, and it pops up in a lot of practical situations. So, if you're ready to get a better handle on how to work out the dimensions of these interesting figures, we’re about to walk through the exact steps and the very formula that makes it all possible. It’s pretty much about taking the average of two lengths and then multiplying by how tall the shape stands.
Table of Contents
- What is a Trapezoid, Anyway?
- Getting to Know the Trapezoid Area Formula Components
- How Do You Figure Out the Trapezoid Area Formula?
- Why Does the Trapezoid Area Formula Work?
- Putting the Trapezoid Area Formula to Use: A Walk-Through
- What Are Some Common Uses for the Trapezoid Area Formula?
- Is There More Than One Way to Express the Trapezoid Area Formula?
- Making Sense of the Trapezoid Area Formula
What is a Trapezoid, Anyway?
Before we jump into figuring out how much surface a trapezoid covers, it’s probably a good idea to, you know, get a clear picture of what a trapezoid actually is. Basically, it’s a four-sided flat shape, which we call a quadrilateral. What makes it special, and sets it apart from other four-sided figures like rectangles or parallelograms, is that it only has one set of sides that run side-by-side, never meeting. These parallel sides are what we refer to as the "bases" of the trapezoid. The other two sides are not parallel, and they typically slant. You can find these shapes everywhere, like the side view of a simple bucket, or maybe a certain kind of roof line on a building. It's a shape that's, like, quite common in the things we build and see around us, so understanding its properties is pretty helpful.
Think of it this way: imagine two parallel lines, like train tracks. Now, draw two other lines that connect those tracks, but at an angle, so they aren't parallel to each other. What you’ve just created is, essentially, a trapezoid. The distance between those two parallel sides, measured straight across, is what we call the height of the trapezoid. This height is really important for figuring out its area, as we’ll see very soon. So, in some respects, it’s a shape that has a clear top and bottom, or two distinct ends, that are perfectly aligned, even if the other parts are a bit more crooked.
It’s kind of a fun shape to think about because it’s not as rigid as a square, but it still has a lot of structure. The two parallel sides can be different lengths, which is why it looks a bit tapered. This difference in length between the two bases is actually a key part of why the trapezoid area formula works the way it does. We’re essentially going to be finding an average measurement for those two parallel sides, which, you know, makes a lot of sense when you think about it. It’s like trying to find the middle ground between two different measurements, which is pretty clever, actually.
Getting to Know the Trapezoid Area Formula Components
To really get a handle on the trapezoid area formula, it helps to break down its parts. There are, basically, three main pieces of information you need to gather. First, you have the two parallel sides, which we call the bases. It doesn't really matter which one you call 'base 1' and which one you call 'base 2' – some people use 'a' and 'b' for these, which is, you know, perfectly fine. What’s important is that you have the measurement of both of them. These are the lengths of the top and bottom edges, so to speak, of your trapezoid. Without these, you can’t even begin to figure out the space inside.
Next up, you need the height of the trapezoid. This isn’t just any side length; it’s the straight-up-and-down distance between those two parallel bases. Imagine dropping a plumb line from one base to the other, making a perfect right angle with both of them. That measurement is your height, often represented by the letter 'h'. It’s really important that this measurement is perpendicular to the bases, otherwise, your calculations for the trapezoid area formula won’t be quite right. So, you know, always look for that straight, shortest distance between the parallel lines. It’s pretty much the 'altitude' of the shape, as some folks might say.
So, to sum up, you’ve got: the length of one parallel side (let's say 'a'), the length of the other parallel side (let's say 'b'), and the straight distance between them ('h'). These three numbers are the ingredients for our trapezoid area formula. Once you have these measurements, putting them into the formula is, honestly, the easiest part. It’s kind of like having all the pieces of a simple puzzle; once you know where they go, the picture just, you know, comes together quite naturally. This basic setup is what makes the whole process pretty straightforward.
How Do You Figure Out the Trapezoid Area Formula?
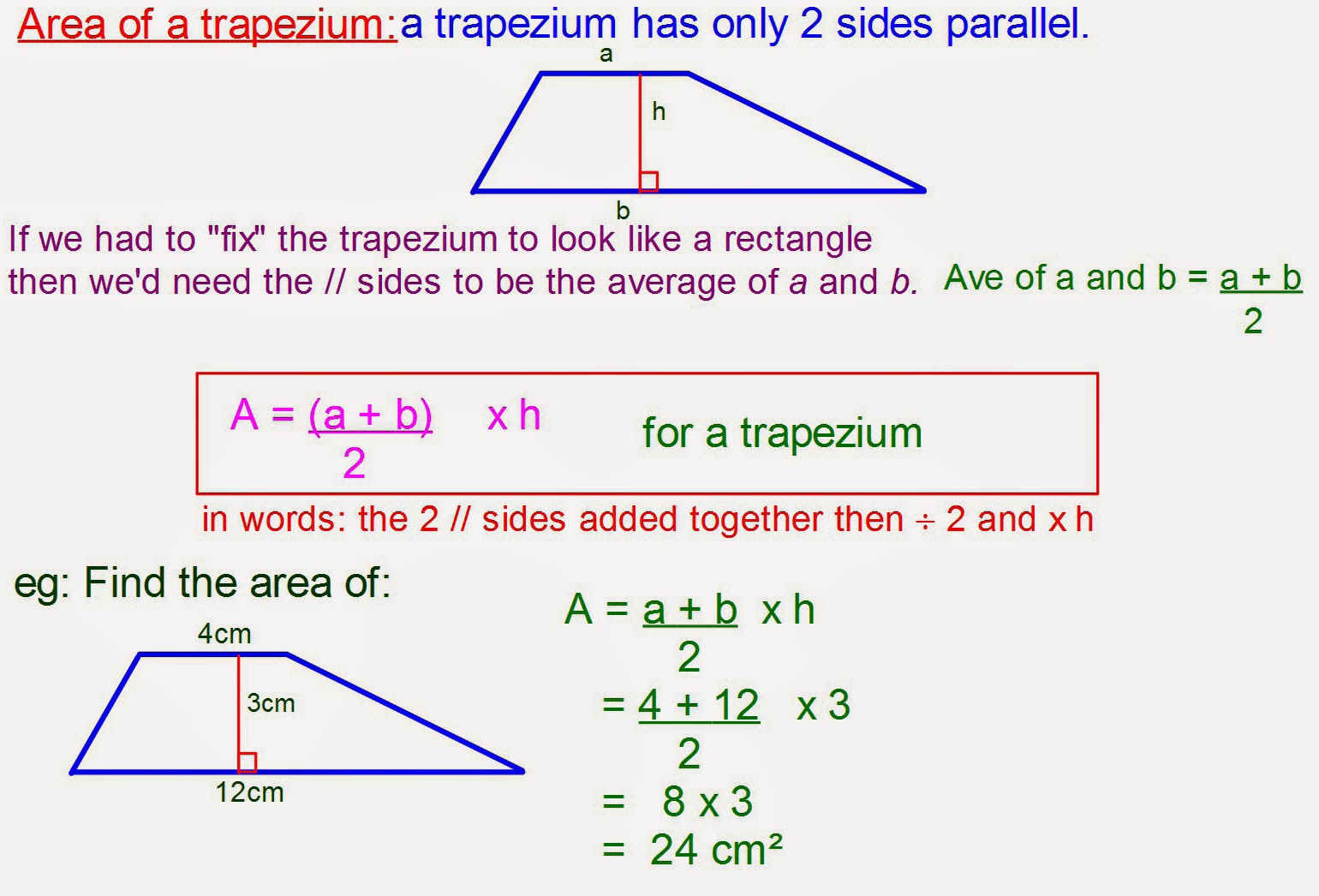
Alright, so you’ve got your trapezoid, and you’ve identified its two parallel sides, the bases, and its height. Now comes the fun part: putting it all together to figure out how much space it takes up. The way to do this is with a very specific, yet quite simple, rule for measurement. The most common way to write it down is: A = ½ (a + b)h. Here, 'A' stands for the area, which is the total surface inside the shape. The 'a' and 'b' are those lengths of the parallel sides we just talked about, and 'h' is the height, that straight distance between them. It's, you know, a pretty compact way to express something quite powerful.
Let's break down that trapezoid area formula a little more, just to make sure it’s super clear. The first thing you do is add the lengths of the two bases together. So, you take 'a' and you add 'b' to it. This gives you a combined length. Then, you take that combined length and you multiply it by the height, 'h'. Finally, you take that whole result and you multiply it by one-half, or, you know, simply divide it by two. That last step is actually pretty important because it accounts for the fact that a trapezoid isn't a simple rectangle. It's, like, taking an average of the two bases before you multiply by the height, which is a neat trick.
So, in practice, if your top base is 4 units long, your bottom base is 6 units long, and the height is 3 units, you would first add 4 and 6, which gives you 10. Then you multiply that 10 by the height, 3, which makes 30. And finally, you take half of 30, which is 15. So, the area of that particular trapezoid would be 15 square units. It’s really that simple, you know? The trapezoid area formula is, pretty much, a step-by-step instruction manual for finding that surface measurement. It's not nearly as complex as some other geometric formulas, which is, you know, a real plus.
Why Does the Trapezoid Area Formula Work?
You might be wondering why the trapezoid area formula is set up the way it is. Why do we add the bases and then divide by two? Well, it’s actually a rather clever way of turning a tricky shape into something more familiar. Think about it this way: if you take two identical trapezoids and flip one upside down, then put them together, what do you get? You get a parallelogram! And finding the area of a parallelogram is pretty straightforward: it’s just its base multiplied by its height. So, you know, this is kind of a visual proof of why the formula makes sense.
When you combine those two trapezoids to form a parallelogram, the base of that new, larger shape is actually the sum of the two bases of your original trapezoid (a + b). The height stays the same. So, the area of that big parallelogram would be (a + b) multiplied by h. But remember, you used *two* trapezoids to make that parallelogram. So, to find the area of just *one* trapezoid, you simply take half of the parallelogram’s area. That’s where the "½" comes from in the trapezoid area formula. It’s, you know, pretty elegant when you think about it, turning something complex into something simpler.
Another way to look at it is that adding the two bases and dividing by two gives you the "average" length of the bases. Imagine if your trapezoid could somehow be squeezed or stretched into a rectangle that has the same height, but its length is that average base measurement. The area of that "average" rectangle would be its length (the average of 'a' and 'b') multiplied by its height. And that's, basically, what the trapezoid area formula does. It finds the average width of the shape and then multiplies it by its height. It’s a concept that, you know, applies to many areas of measurement, not just geometry, so it’s pretty useful to grasp.
Putting the Trapezoid Area Formula to Use: A Walk-Through
Let's actually walk through an example, just to make sure the trapezoid area formula feels really clear and easy to use. Imagine you have a garden bed shaped like a trapezoid. One of its parallel sides is 8 feet long, and the other parallel side is 12 feet long. The straight distance between these two parallel sides, its height, is 5 feet. So, we have our 'a' as 8 feet, our 'b' as 12 feet, and our 'h' as 5 feet. You know, these are pretty typical measurements you might encounter in a real-world situation.
The first step, as the trapezoid area formula suggests, is to add the lengths of the two bases together. So, we take 8 feet and add 12 feet, which gives us a total of 20 feet. This 20 feet is, like, the combined length of the parallel sides. It’s the sum of 'a' and 'b'. This part is, honestly, super straightforward, just simple addition. There's nothing complicated about it at all, which is pretty nice.
Next, we take that sum, 20 feet, and multiply it by the height, which is 5 feet. So, 20 multiplied by 5 gives us 100. This 100 is, basically, what you’d get if you had a rectangle with a base of 20 feet and a height of 5 feet. But remember, we’re dealing with a trapezoid, so we have one more step to go. It’s, you know, pretty much like setting up the problem for the final calculation, so we’re getting closer to our actual area.
Finally, we take that 100 and multiply it by one-half, or, you know, divide it by 2. So, 100 divided by 2 equals 50. This means the area of our trapezoid-shaped garden bed is 50 square feet. It’s really that simple! The units for area are always "square units" because you’re measuring a two-dimensional surface. So, whether it’s square feet, square meters, or square inches, you always specify that. The trapezoid area formula just guides you through these steps, making it pretty easy to figure out the space involved.
What Are Some Common Uses for the Trapezoid Area Formula?
It might seem like just a math problem, but the trapezoid area formula actually has a lot of practical uses in the world around us. Think about architecture, for instance. Many roofs are designed with slopes that create trapezoidal shapes when viewed from the side. Builders and architects need to figure out the surface area of these sections to know how much material, like shingles or insulation, they'll need. So, you know, it’s not just for textbooks; it’s for real construction work, which is pretty cool.
Beyond buildings, consider land surveying. Sometimes, a plot of land isn't a perfect square or rectangle. It might have irregular boundaries, and some sections could very well be trapezoidal. Surveyors use this formula to accurately measure the acreage or square footage of these land parcels. This is, you know, really important for property deeds and for planning how to use the land. It’s about getting precise measurements for something that, you know, might look a bit messy at first glance.
Even in fields like engineering, the trapezoid area formula comes into play. For example, when calculating the cross-sectional area of a canal or a ditch, which might have sloped sides, a trapezoidal shape is often used as a model. This helps engineers figure out how much water can flow through or how much earth needs to be moved. It’s, like, a fundamental tool for understanding volumes and capacities in various design and construction projects. So, it's pretty versatile, actually.
And then there's design and crafts. If you're cutting fabric for a quilt, or designing a piece of furniture, or even drawing a graphic for a website, you might encounter trapezoidal elements. Knowing how to calculate their area helps you plan your materials efficiently and ensure your designs are accurate. It’s, you know, pretty much about having the right tools for the job, and this formula is definitely one of them. It's a skill that, you know, just makes sense to have in your toolbox for many different creative pursuits.
Is There More Than One Way to Express the Trapezoid Area Formula?
You might see the trapezoid area formula written down in slightly different ways, but don't let that confuse you. The core idea is always the same. Sometimes, instead of 'a' and 'b' for the bases, you might see 'b1' and 'b2'. This just means "base one" and "base two," which, you know, makes it pretty clear that you're dealing with two different parallel sides. So, the formula would look like: A = ½ (b1 + b2)h. It’s, basically, the same thing, just with different labels for the base measurements.
Another common way you might spot it is with the multiplication sign explicitly written out, or with the order slightly rearranged. For example, you could see: A = h × (b1 + b2) / 2. Or even: A = (b1 + b2) / 2 × h. All these variations are, you know, mathematically identical. The order of multiplication doesn't change the final answer, and dividing by 2 is the same as multiplying by ½. So, really, it’s just a matter of how someone chooses to write it down, which is pretty flexible.
The key takeaway is that no matter how it's presented, the essential components remain constant: you always need the lengths of the two parallel bases and the straight distance between them (the height). As long as you have those three pieces of information, and you apply the concept of averaging the bases and then multiplying by the height, you’ll arrive at the correct area. So, you know, don't get too hung up on the exact symbols used, just focus on the actual operations. It’s, pretty much, about understanding the underlying process, which is quite logical.
Making Sense of the Trapezoid Area Formula
So, there you have it – the trapezoid area formula, broken down into its simple, understandable parts. It’s a way to figure out the space covered by a shape that has one pair of parallel sides. You just need to know the measurements of those two parallel sides, which we call the bases, and the straight distance between them, which is the height. Once you have those three numbers, you add the bases together, divide that sum by two (to get the average base length), and then multiply that average by the height. It’s, you know, a pretty neat little trick that helps us measure all sorts of things.
This formula, A = ½ (a + b)h, is a fundamental piece of geometry that, honestly, comes in handy more often than you might think. From designing buildings to planning garden layouts, or even just understanding the shapes around you, knowing how to work with trapezoids gives you a bit more insight into the world. It’s a testament to how simple mathematical ideas can be incredibly powerful tools for solving real-world problems. So, next time you spot a trapezoid, you’ll, pretty much, know exactly how to figure out its dimensions.
The beauty of this particular way of figuring things out is its straightforwardness. It doesn't require any fancy tools or really complex calculations. Just a few basic measurements and some simple arithmetic. It’s, like, a perfect example of how geometry helps us make sense of the physical world by providing clear, step-by-step methods for measurement. So, you know, it’s pretty satisfying to be able to look at a shape and instantly know how to approach figuring out its area, all thanks to this handy trapezoid area formula.
This article has walked you through what a trapezoid is, the different parts of the trapezoid area formula, how to apply the formula with an example, why the formula works, and some everyday situations where it’s useful. We also looked at how the formula might be written in slightly different ways while still meaning the same thing. The goal was to make this geometric concept feel approachable and easy to grasp, showing that figuring out the area of a trapezoid is, you know, pretty much a simple process once you understand its components.

Lesson Video: Area of a Trapezoid | Nagwa
Trapezoid Area

Area Formula Trapezoid Shapes Area Formulas Stock Vector (Royalty Free